圆钢管单向压弯构件稳定

来源：许磊, 童根树. 圆钢管单向压弯构件稳定[J]. 钢结构(中英文), 2021, 36(9): 1-9. 

doi: 10.13206/j.gjgS20111601

点击阅读全文

研究背景

       对柱端无很大横向力或集中弯矩作用的圆钢管压弯构件, GB 50017—2017《钢结构设计标准》中采用式(1)计算其整体稳定承载力:

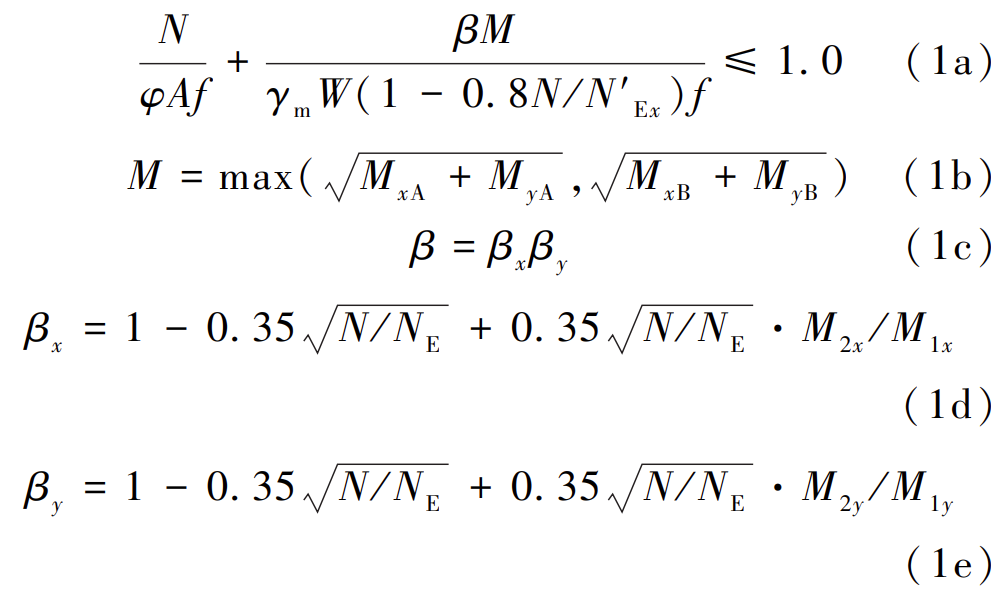
       式中: φ 为轴心受压构件的整体稳定系数; γm 为截面塑性发展系数; M 为计算双向压弯整体稳定时采用的弯矩值; NE 为根据构件最大长细比计算的欧拉力; β 为等效弯矩系数,当圆管柱仅为平面内压弯时, β  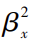= ; N′Ex 为考虑抗力分项系数后的欧拉临界承载力; W 为弯矩作用平面内对受压最大纤维的毛截面模量; f 为钢材强度设计值; MxA、MyA、MxB、MyB 分别为 A、B端对应的 x、y 轴的弯矩; M1x、M2x、M1y、M2y 分别为构件两端关于 x、y 轴的最大、最小弯矩,构件无反弯点时取同号,有反弯点时取异号,并满足 |M1x| ≥ |M2x|、|M1y| ≥ |M2y| 。

       对比工字钢截面,圆管截面是没有角点的闭口截面,截面任意对称且抗弯刚度较大,所以圆钢管压弯构件这种特殊的截面特性可能导致其具有与工字钢压弯构件不同的轴向压力-弯矩相关关系。国外部分规范中并没有为圆管截面提出特殊形式的相关计算公式,我国 GB 50017—2017 中虽然将圆管截面作为特殊截面处理并采用式(1)计算圆钢管压弯构件稳定承载力,但是对于端部弯矩比为1的圆钢管单向压弯构件,式(1)的形式与工字钢单向压弯构件稳定承载力计算公式形式相同,仅仅是塑性发展系数和稳定系数等常数的取值不同,可能并不能体现出圆钢管单向压弯构件轴向压力-弯矩相关关系与工字钢单向压弯构件的区别,所以有必要对圆钢管单向压弯构件进行深入研究。

       本文采用 ANSYS 有限元程序对圆钢管单向压弯构件进行计算,并将有限元计算结果与式(1)计算结果对比,讨论式(1)对计算圆钢管单向压弯构件稳定承载力的适用性。本文从圆钢管截面塑性铰状态的轴力-弯矩相关关系出发,推导出圆钢管单向压弯构件极限承载力上限的理论公式,并参考该计算公式对大量有限元数据进行拟合,提出更适合圆钢管单向压弯构件极限承载力的理论计算公式。

研究内容

1 非线性有限元计算

1.1 计算方法

       本文采用 ANSYS 有限元程序计算圆钢管单向压弯构件的稳定极限承载力。有限元模型采用 Beam189 单元,该单元是一种基于 Timoshenko 梁理论的3D二次有限应变梁单元,考虑剪切应变的影响,每个单元有3个节点,每个节点有6或7个自由度,因此该单元可以准确地计算构件整体稳定承载力。

       有限元建模时考虑初弯曲和残余应力对构件稳定极限承载力的影响。初弯曲在平面内按照正弦半波考虑,幅值 δ = L /1000( L 为构件长度)。残余应力只考虑热轧圆钢管纵向残余应力,采用的残余应力分布模型如图 1所示,管壁外侧压应力为-0.15f ,管壁内侧拉应力为0.15f。通过前期有限元分析,得出相同长细比下不同的径厚比 D/t ( D 为截面外直径, t 为截面厚度)对圆钢管单向压弯构件的 N/(φNP)-M/MP ( NP 为截面塑性极限轴力, MP 为截面塑性极限弯矩)相关关系影响极小,故本次采用的模型截面直径 D =360 mm,径厚比 D/t =60。钢材构采用理想弹塑性模型,弹性模量 E =206 GPa,钢材型号采用 Q235、 Q355 和 Q460。蔡春声等指出压力和弯矩交叉作用时,改变加载顺序对于构件的极限承载力影响很小;许磊通过有限元软件对不同长细比下改变加载顺序的圆钢管单向压弯构件进行计算,发现不同加载顺序对圆钢管单向压弯构件的 N/(φNP)-M/MP 相关关系的影响极小,故本文采用先加轴力再加弯矩的加载顺序,构件受力模型如图 2 所示。

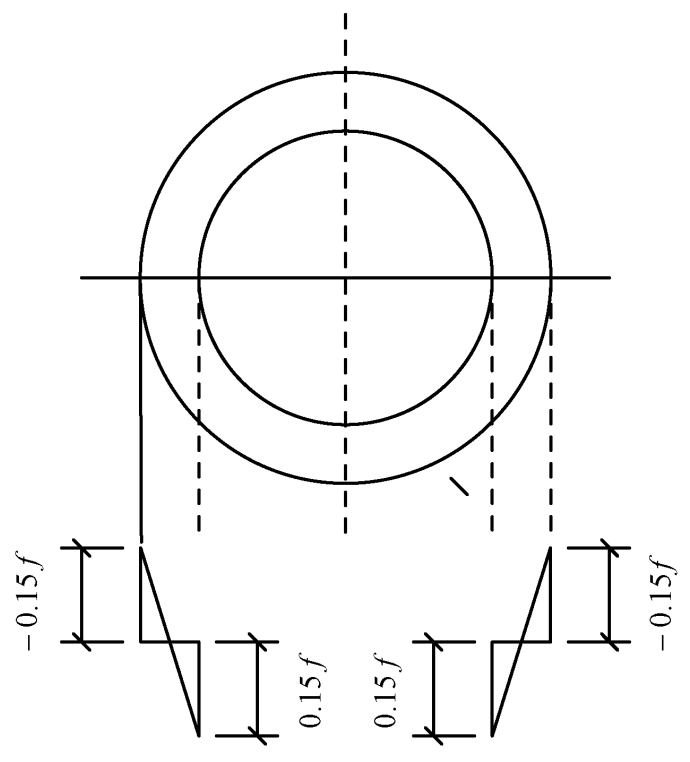
图 1 圆钢管截面纵向残余应力分布模型

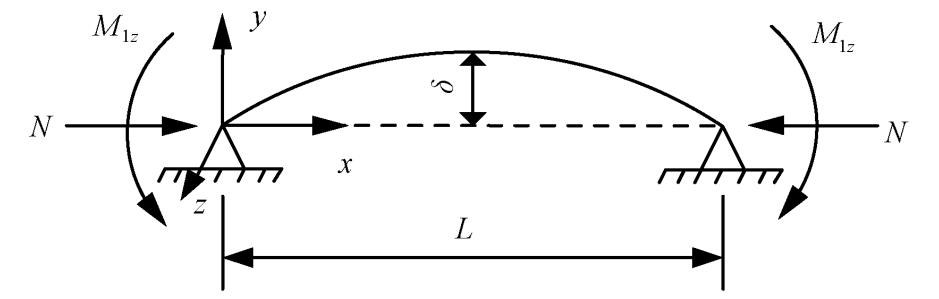
图 2 压弯杆受力简图

1.2 计算结果与分析

式(2)是 GB 50017—2017 中圆钢管压弯构件的强度控制公式:

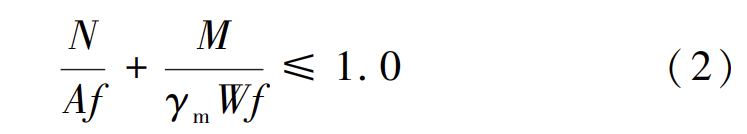
记则不考虑抗力分项系数的式(1)可等效表示为式(3a):

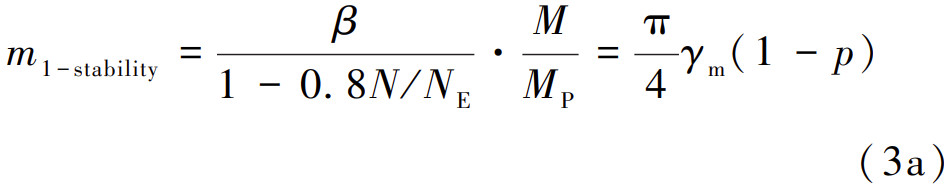
同样,强度式(2)也可等效表示为式(3b):

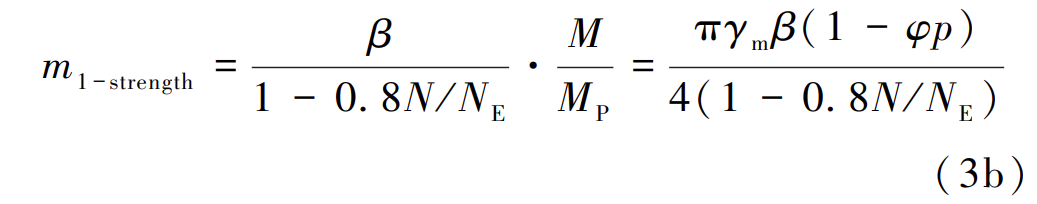
有限元求解的极限弯矩为 MFE(p) ,记 mFE = 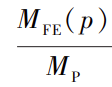,则 m1 用有限元计算结果可以表示为:

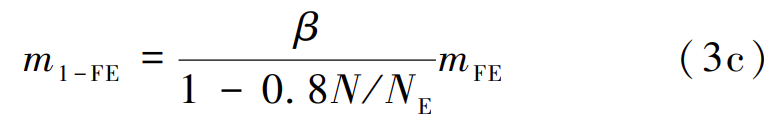
       因为压弯构件在两端弯矩比较小或者异号时可能会发生强度破坏,所以需要判定有限元的数据点是由强度公式控制还是由稳定公式控制。判定方法如下:当在相同 p 下,若式(3a)计算的 m1-stability 大于式(3b)计算的 m1-strength ,说明这种情况下构件破坏是由强度控制的,反之,构件破坏是由稳定控制;记式(3a)等于式(3b)时的轴力为 plimit ,当 p ≤ plimit 时,构件破坏由强度式(2)控制;当 p > plimit 时,构件破坏由稳定式(1)控制。如图 3 所示,横坐标为 m1,图中式(3a)曲线在式(3b)曲线下方时,构件破坏由稳定公式(3a)控制,对应的有限元数据点是式(3c)曲线的稳定控制部分;式(3a)曲线在式(3b)曲线上方时,构件破坏由强度式(3b)控制,对应的有限元数据点是式(3c)曲线的强度控制部分。

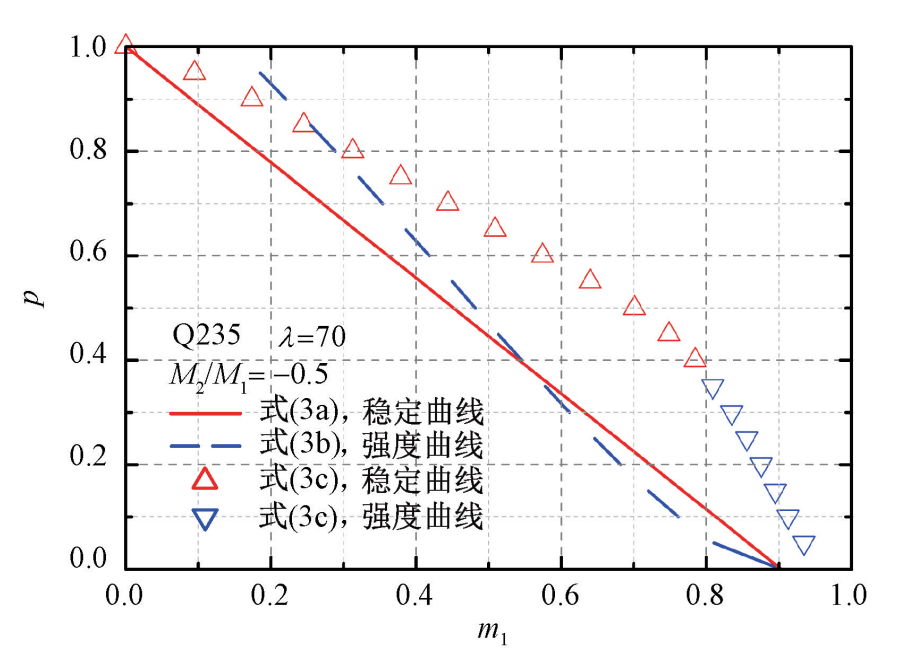
注: λ 为长细比; M1 为较大端部弯矩; M2 为较小端部弯矩。

图 3 稳定公式(3a)及强度公式(3b)与有限元公式对比

       图4~图6是有限元计算结果与式(3a)的对比,图中是参考式(3)将式(1)、式(2)和有限元计算结果的横坐标均变换为 m1 ,图中式(3c)曲线即为横坐标变换后的弯矩比从-1到1的有限元计算结果,式(3a)结果即横坐标变换后的稳定公式(1),参考图3的形式只保留了由稳定公式(1)控制的有限元结果并删除了由强度公式(2)控制的有限元结果。从图中可以看出,式(3a)的计算结果对于有限元计算结果整体上是过于保守的。两端弯矩比为1且长细比大于60时,式(3a)的计算结果与有限元计算结果比较接近;长细比不大于30时,式(3a)则偏安全较多。不同弯矩比情况下有限元计算结果与式(3a)计算结果存在不同程度的偏差,尤其构件是双曲率弯曲的情况下,两者偏差较大。相同长细比和弯矩比下,不同轴力的式(3a)计算结果的保守程度也不一样,一般而言,轴力较小的情况下,式(3a)会更加保守。所以有必要针对圆钢管单向压弯构件进行研究,提出更适合于该构件的稳定承载力计算公式。

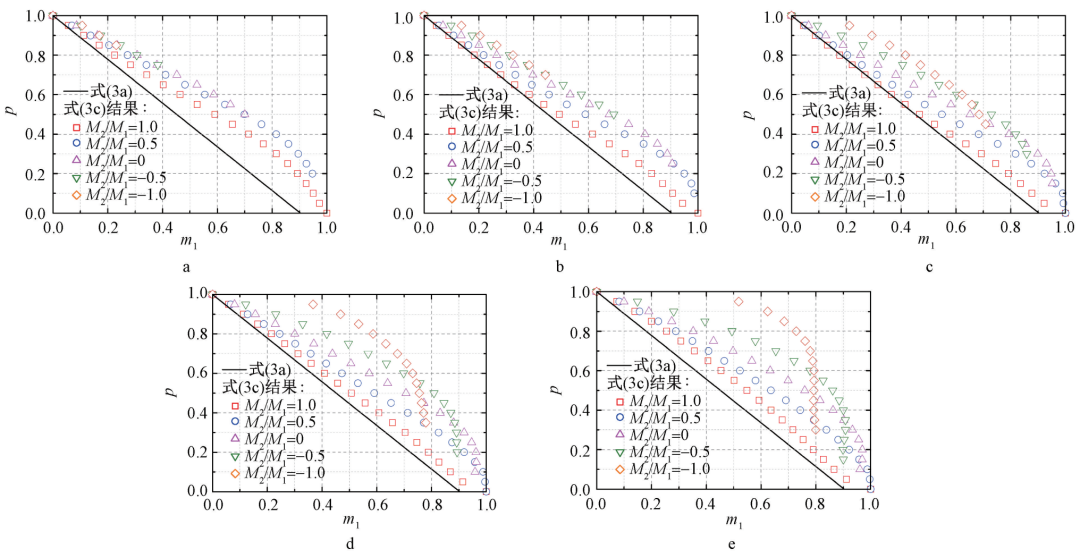
a—长细比 λ =30; b—长细比 λ =60; c—长细比 λ =90; d—长细比 λ =120; e—长细比 λ =150。

图 4 Q235 钢材的有限元结果与式(3a)结果的对比

a—长细比 λ =30; b—长细比 λ =60; c—长细比 λ =90; d—长细比 λ =120; e—长细比 λ =150。

图 5 Q355 钢材的有限元结果与式(3a)结果的对比

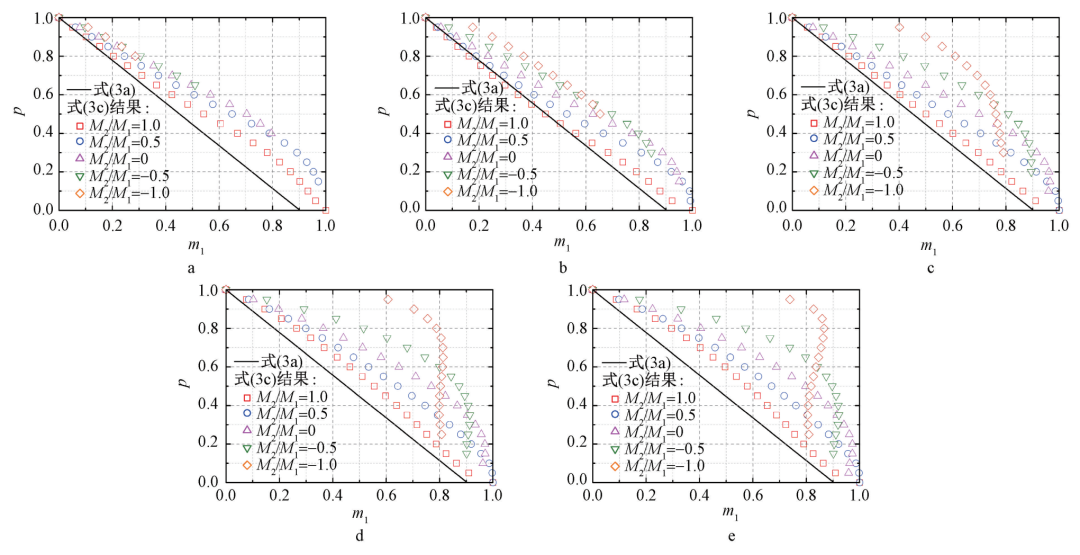
a—长细比 λ =30; b—长细比 λ =60; c—长细比 λ =90; d—长细比 λ =120; e—长细比 λ =150。

图 6 Q460 钢材的有限元结果与式(3a)结果的对比

2 理论分析与有限元结果对比

2.1 轴力-弯矩相关公式的理论推导

首先推导圆钢管截面塑性铰状态的轴力-弯矩相关关系。如图7所示,图中阴影部分表示受压塑性区,由此可以得到:

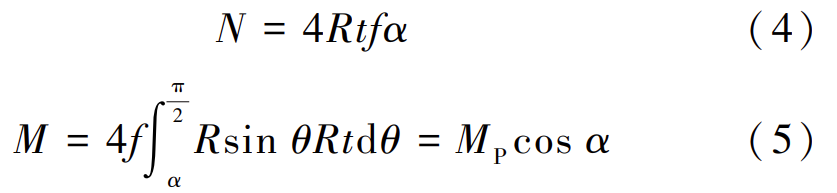
消去 α 后得到圆钢管截面塑性铰状态的精确轴力-弯矩相关关系:

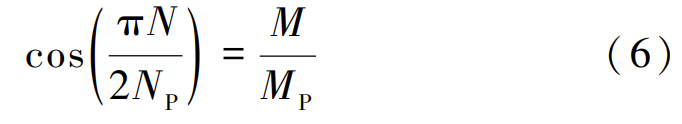
其中  NP = 2πRtf, MP = 4R2tf 

如图8所示,式(6)可以用式(7)近似表示:

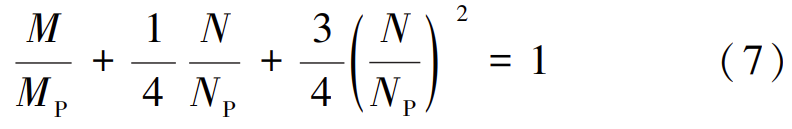
将单向压弯构件存在的三种初始缺陷等效为初始弯曲 e0 ,把等效初始弯曲放大后的弯矩和纯弯弯矩放大后代入式(7),得到式(8):

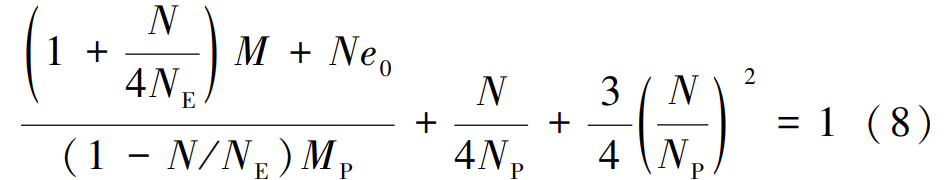
当外弯矩 M 等于零时,轴心受压杆件的极限承载力 Nu0 = φNP ,代入式(8)后得:

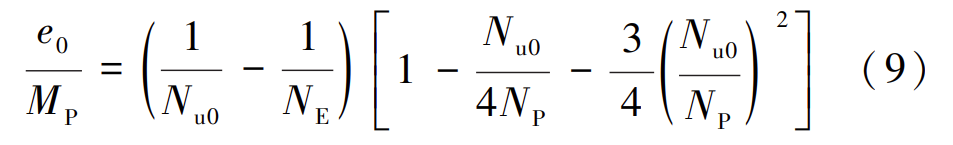
将式(9)代入式(8)后得:

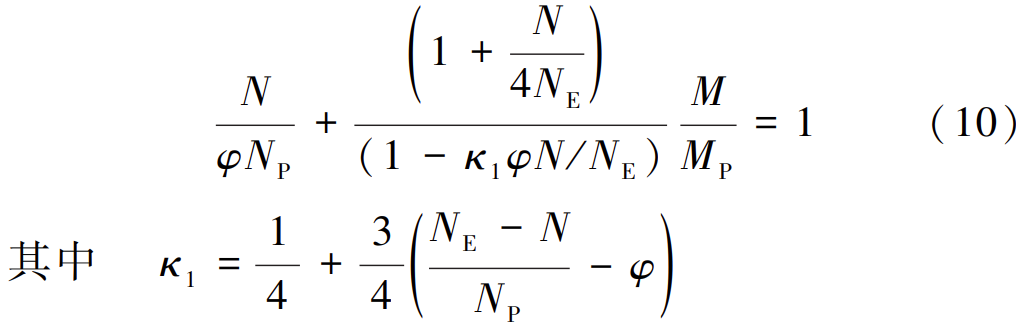
       式(10)是从圆管截面的塑性铰极限承载力公式出发推导出的圆钢管单向压弯构件稳定承载力公式,是承载力的上限。通过对大量圆钢管单向压弯构件进行有限元分析,将有限元计算结果以式(10)为基础进行拟合,并对线性变化弯矩引入 GB50017—2017 中对工字钢截面已经采用的等效弯矩系数,得到式(11):

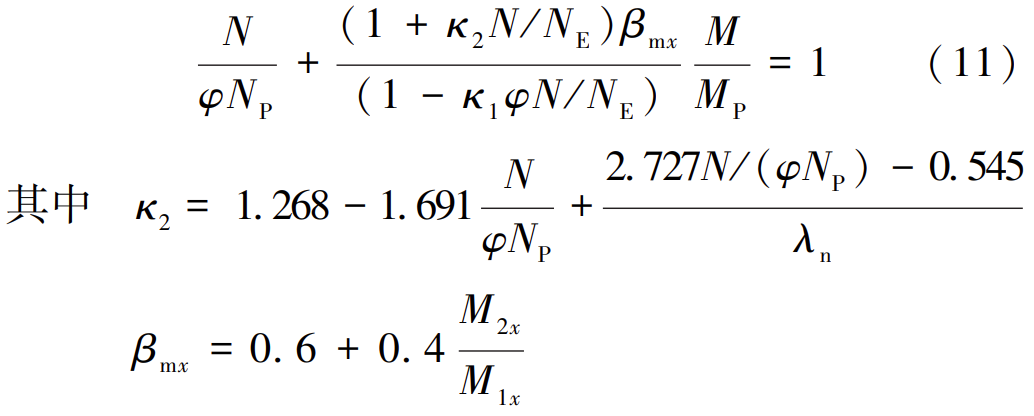
式中: λn 为正则化长细比。

与纯理论推导的式(10)相比,式(11)仅在 κ2 系数上根据有限元分析的结果进行了拟合。

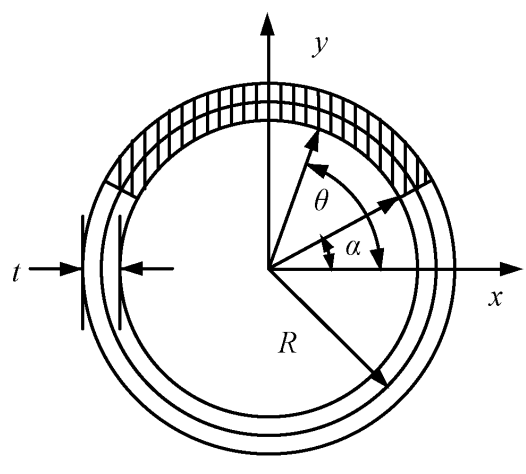
图 7 截面参数示意

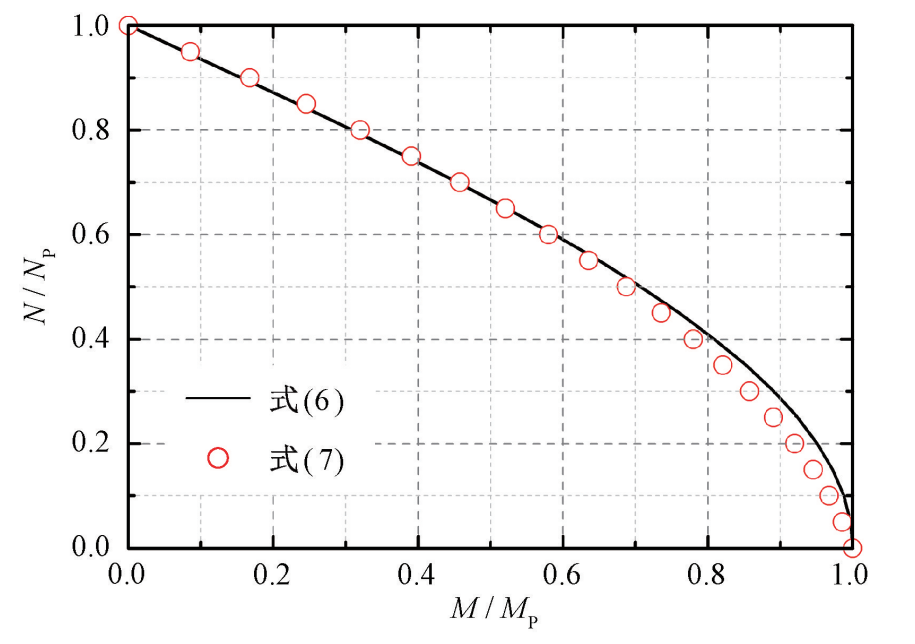
图 8 式(6)与式(7)对比

       图9是 Q235 强度且弯矩比等于1情况下的不同长细比下圆钢管单向压弯构件的有限元计算曲线及由式(1)、式(10)和式(11)计算的轴力-弯矩曲线。从图 9a有限元结果的轴力-弯矩曲线中可以看出,随着长细比由30增大到150,有限元计算曲线整体上是由向上凸出逐渐变为向下凹陷;当长细比小于50时,有限元计算曲线整体基本是向上凸出的,当长细比大于50时,有限元计算曲线整体上是向下凹陷的;当长细比小于70时,有限元计算曲线除了整体上的凹凸性特点外还存在细部凹凸性变化,即长细比小于70的构件,有限元计算曲线存在反弯点,当轴力较小时,有限元计算曲线向上凸出,当轴力较大时,有限元计算曲线向下凹陷。图9b 是式(1)的轴力-弯矩曲线,可以看出,式(1)曲线是向下凹陷的,并且随着长细比增大,向下凹陷程度逐渐变大;长细比小于50时,有限元计算的轴力-弯矩曲线整体上是向上凸出的,而式(1)曲线是向下凹陷的且没有体现出反弯点的特点;再结合图4~图6,进一步说明了式(1)偏保守但是并没有很好地反映圆钢管单向压弯构件的轴力-弯矩曲线形状,尤其是在小长细比的情况下。图9c是未修正的理论推导公式(10)的轴力-弯矩曲线,可以看出:式(10)在整体的凹凸性上与有限元计算曲线是基本一致的,凹凸程度差距并不大,但长细比小于70时,式(10)曲线仍没有体现出反弯点的特点。图9d是式(11)的轴力-弯矩曲线,可以看出,该式曲线在整体凹凸性上与有限元计算曲线保持一致,且在长细比小于70 时,式(11)的曲线也体现出反弯点的特点。综合来看,在弯矩比等于1的情况下,式(10)可以在整体上表示圆钢管单向压弯构件的轴力-弯矩关系曲线形状,而对单个参数拟合修正后提出的式(11)则反映了圆钢管单向压弯构件的真实轴力-弯矩关系曲线形状,故式(11)作为其稳定承载力计算公式的基础是合适的。

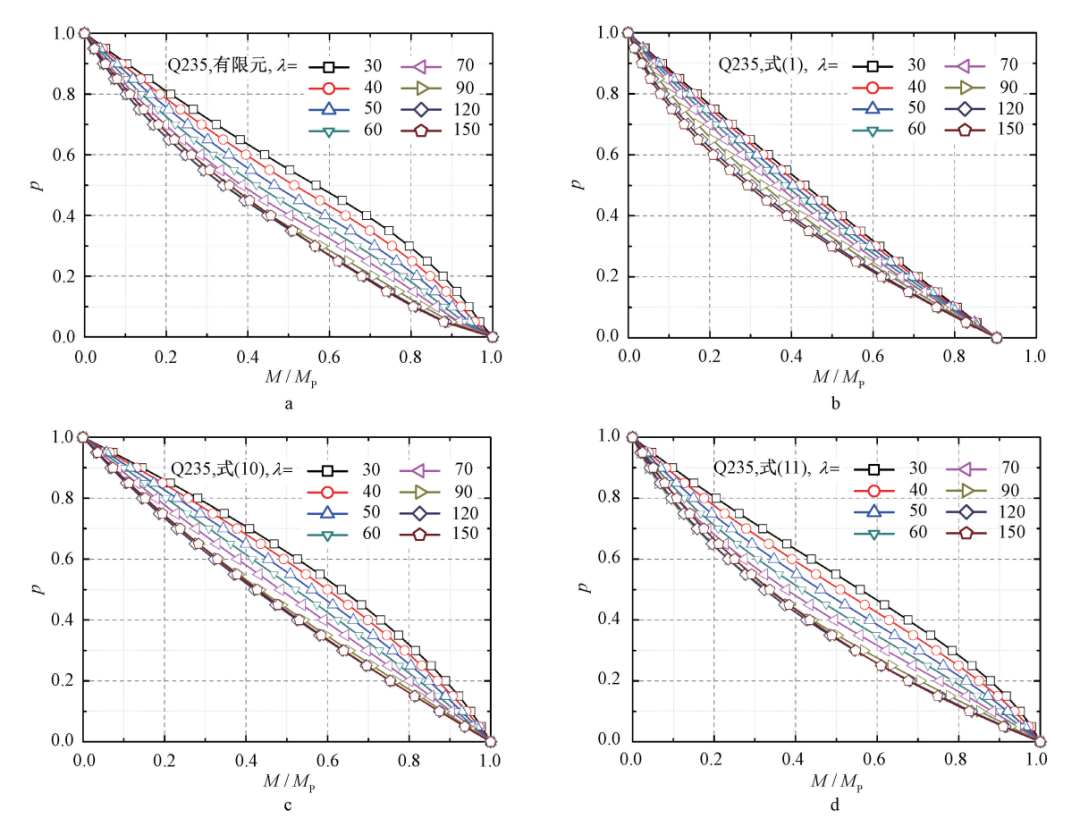
a—有限元结果; b—式(1); c—式(10); d—式(11)。

图 9 有限元曲线形状和三个公式的曲线形状

2.2 理论公式与有限元结果对比

基于图9的分析结果,对式(11)与有限元结果进行更加全面的对比。

记,则稳定公式(11)可等效表示为式(12a):

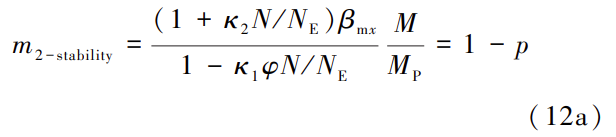
同样,强度公式(6)可等效表示为式(12b):

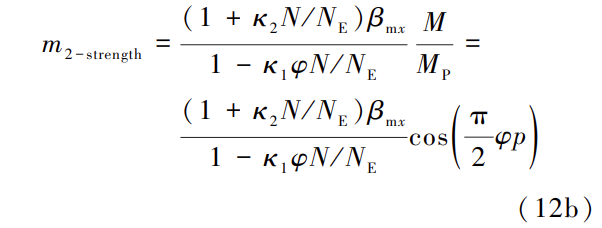
有限元求解的极限弯矩为 MFE(p) ,记 mFE =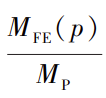,则 m2 用有限元计算结果可以表示为:

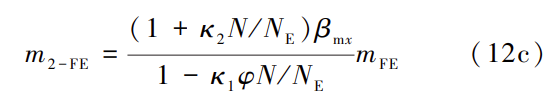
       当在相同 p 下,若式(12a)计算的 m2-stability 大于式(12b)计算的 m2-strength ,就说明这种情况下构件破坏是由强度控制,反之构件破坏是由稳定控制;记式(12a)等于式(12b)时的轴力为 plimit ,当 p ≤ plimit 时,构件破坏由强度公式(6)控制;当 p > plimit 时,构件破坏由稳定公式(11)控制。如图10所示,横坐标为 m2 ,图中式(12a)曲线在式(12b)曲线下方时,构件破坏是由稳定公式(12a)控制的,对应的有限元数据点是式(12c)曲线的稳定控制部分;式(12a)曲线在式(12b)曲线上方时,构件破坏由强度公式(12b)控制,对应的有限元数据点是式(12c)曲线的强度控制部分。

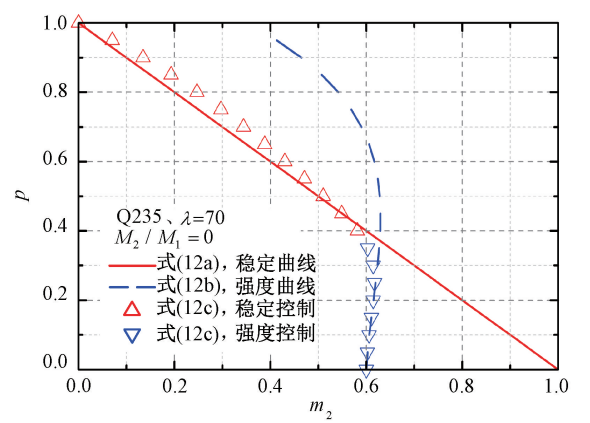
图 10 稳定公式(12a)与强度公式(12b)关系

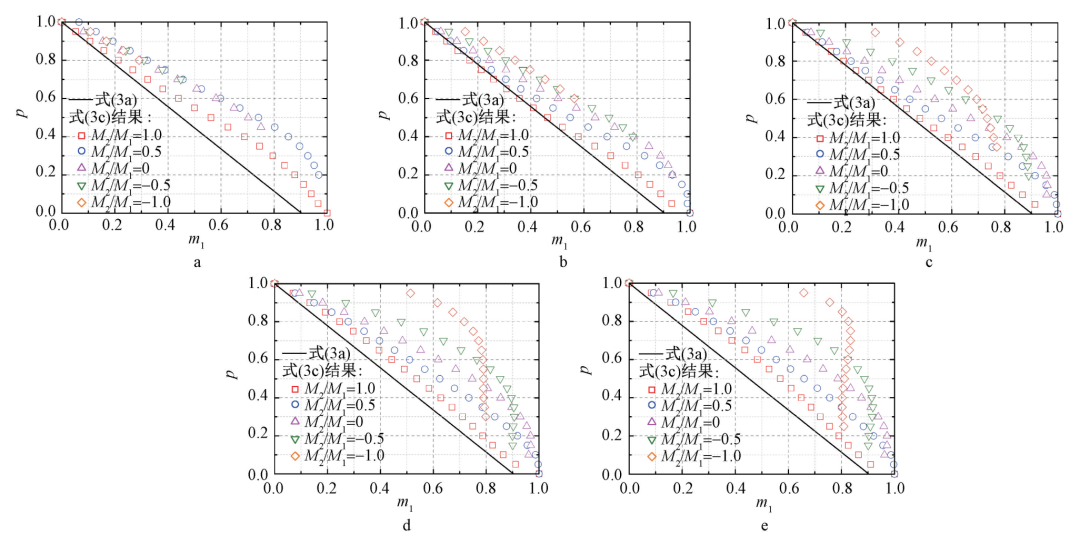
       图11~图13是有限元计算结果与式(12a)计算结果的对比,图中参考式(12)将式(6)、式(11)和有限元计算结果的横坐标均变换为 m2 ,图中式(12c)曲线即横坐标变换后的弯矩比从-1到1的有限元计算结果,式(12a)结果即横坐标变换后的稳定公式(11),参考图3的形式只保留了由稳定公式(11)控制的有限元结果并删除了由强度公式(6)控制的有限元结果。从图11~图13中可看出:式(11)很好表现了圆钢管单向压弯构件的轴向压力-弯矩的相关关系,同时式(11)的计算结果对比有限元计算结果有很好的计算精度;当端部弯矩比为1时,式(11)的计算结果与有限元计算结果吻合很好且整体略偏保守,只有在 p 较小时,式(11)计算结果略低于有限元计算结果,但仍在容许范围之内。对于不等端弯矩作用下的圆钢管单向压弯构件,理论计算公式采用式(11c)计算等效稳定系数,从图中可以看出:该式精度更高, 更加适用于圆管截面。

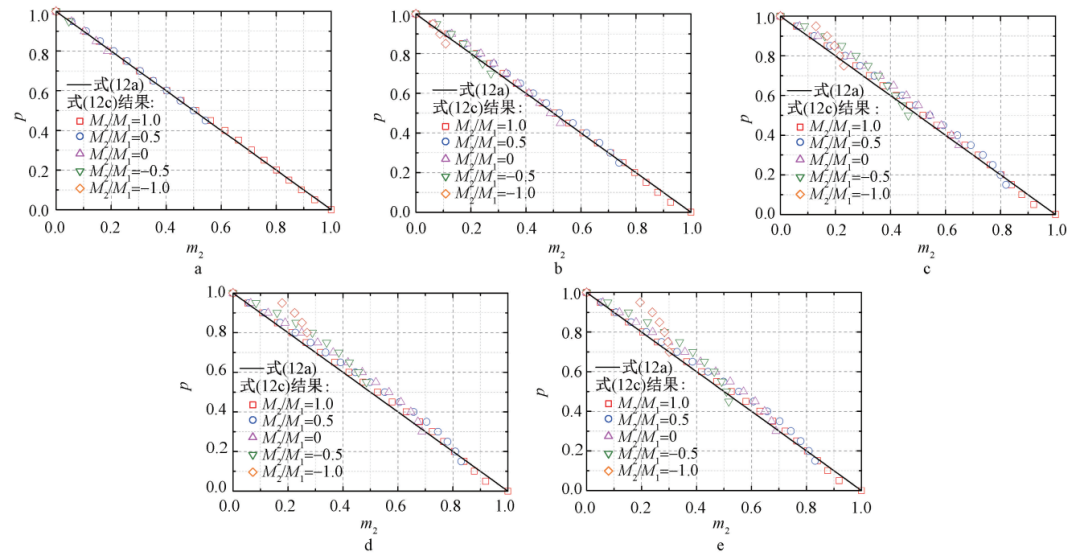
a—长细比 λ =30; b—长细比 λ =60; c—长细比 λ =90; d—长细比 λ 120; e—长细比 λ =150。

图 11 Q235 钢的有限元结果与式(12a)结果的对比

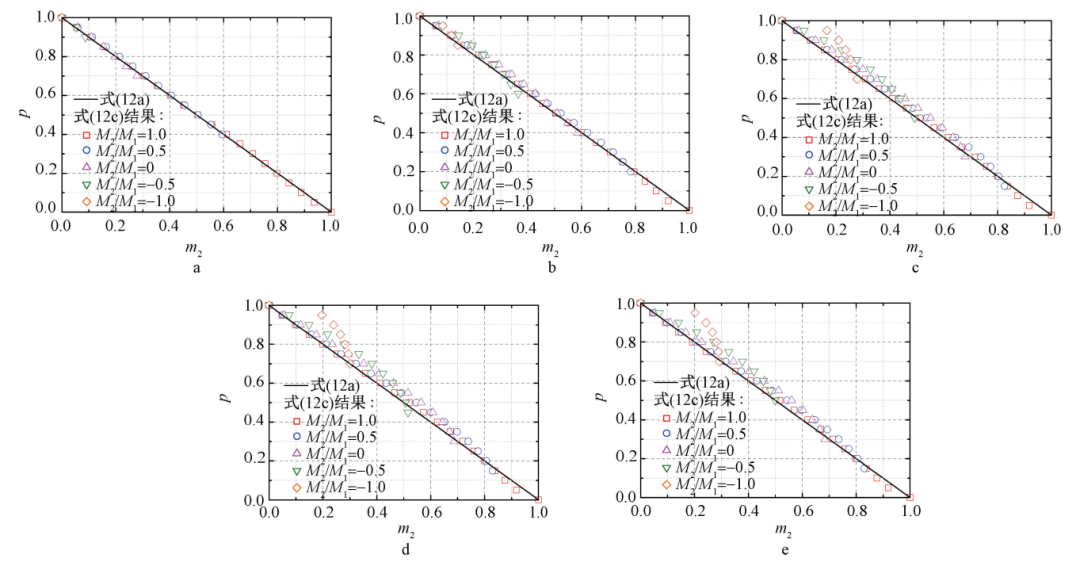
a—长细比 λ =30; b—长细比 λ =60; c—长细比 λ =90; d—长细比 λ =120; e—长细比 λ =150。

图 12 Q355 钢的有限元结果与式(12a)结果的对比

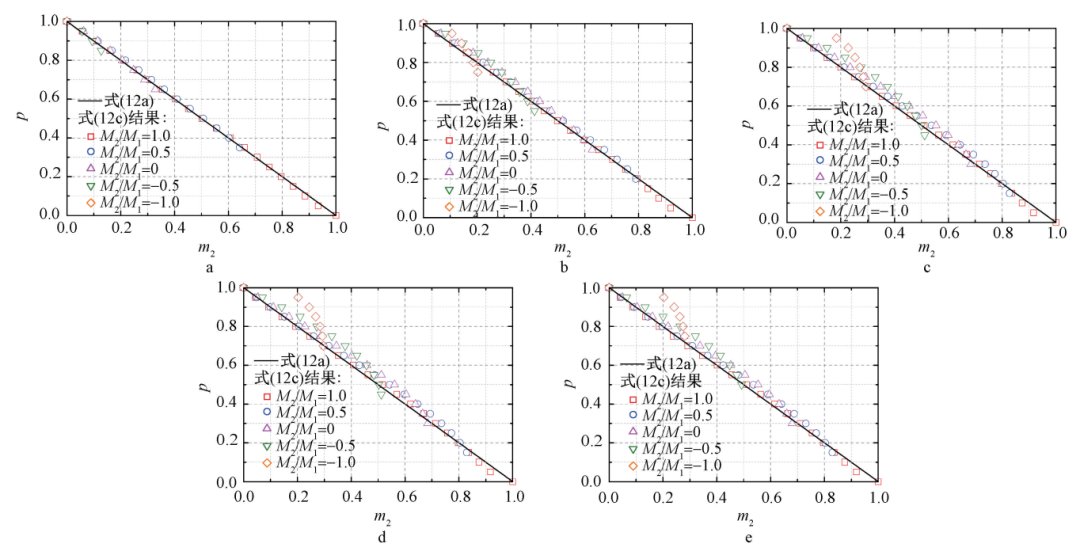
a—长细比 λ =30; b—长细比 λ =60; c—长细比 λ =90; d—长细比 λ =120; e—长细比 λ =150。

图 13 Q460 钢的有限元结果与式(12a)结果的对比

结 论

       对圆钢管单向压弯柱的稳定极限承载力进行理论分析,将有限元计算结果与 GB 50017—2017 中的轴力-弯矩相关公式进行比较,发现 GB 50017—2017 过于保守,尤其是端部弯矩比较小或者是异号的情况。从圆管截面塑性铰状态的轴力-弯矩相关关系出发并代入考虑几何缺陷的弹性二阶弯矩,推导出圆钢管单向压弯柱稳定承载力上限公式,将该式与有限元计算结果进行对比和拟合,修改了理论公式中的一个系数并采用工字钢压弯柱的等效弯矩系数,得到了圆钢管单向压弯柱稳定承载力计算公式,该式适用于计算不同长细比的圆钢管单向压弯柱稳定承载力,且计算结果精度较高。